Entropy of Discrete Conditioned on Continuous Variables

Measure of relative information in probability theory

In information theory, the conditional entropy quantifies the amount of information needed to describe the outcome of a random variable ${\displaystyle Y}$ given that the value of another random variable ${\displaystyle X}$ is known. Here, information is measured in shannons, nats, or hartleys. The entropy of ${\displaystyle Y}$ conditioned on ${\displaystyle X}$ is written as ${\displaystyle \mathrm {H} (Y|X)}$ .

Definition [edit]

The conditional entropy of ${\displaystyle Y}$ given ${\displaystyle X}$ is defined as

${\displaystyle \mathrm {H} (Y|X)\ =-\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)\log {\frac {p(x,y)}{p(x)}}}$

(Eq.1)

where ${\displaystyle {\mathcal {X}}}$ and ${\displaystyle {\mathcal {Y}}}$ denote the support sets of ${\displaystyle X}$ and ${\displaystyle Y}$ .

Note: Here, the convention is that the expression ${\displaystyle 0\log 0}$ should be treated as being equal to zero. This is because ${\displaystyle \lim _{\theta \to 0^{+}}\theta \,\log \theta =0}$ .^[1]

Intuitively, notice that by definition of expected value and of conditional probability, ${\displaystyle \displaystyle H(Y|X)}$ can be written as ${\displaystyle H(Y|X)=\mathbb {E} [f(X,Y)]}$ , where ${\displaystyle f}$ is defined as ${\displaystyle \displaystyle f(x,y):=-\log {\Big (}{\frac {p(x,y)}{p(x)}}{\Big )}=-\log(p(y|x))}$ . One can think of ${\displaystyle \displaystyle f}$ as associating each pair ${\displaystyle \displaystyle (x,y)}$ with a quantity measuring the information content of ${\displaystyle \displaystyle (Y=y)}$ given ${\displaystyle \displaystyle (X=x)}$ . This quantity is directly related to the amount of information needed to describe the event ${\displaystyle \displaystyle (Y=y)}$ given ${\displaystyle (X=x)}$ . Hence by computing the expected value of ${\displaystyle \displaystyle f}$ over all pairs of values ${\displaystyle (x,y)\in {\mathcal {X}}\times {\mathcal {Y}}}$ , the conditional entropy ${\displaystyle \displaystyle H(Y|X)}$ measures how much information, on average, the variable ${\displaystyle X}$ encodes about ${\displaystyle Y}$ .

Motivation [edit]

Let ${\displaystyle \mathrm {H} (Y|X=x)}$ be the entropy of the discrete random variable ${\displaystyle Y}$ conditioned on the discrete random variable ${\displaystyle X}$ taking a certain value ${\displaystyle x}$ . Denote the support sets of ${\displaystyle X}$ and ${\displaystyle Y}$ by ${\displaystyle {\mathcal {X}}}$ and ${\displaystyle {\mathcal {Y}}}$ . Let ${\displaystyle Y}$ have probability mass function ${\displaystyle p_{Y}{(y)}}$ . The unconditional entropy of ${\displaystyle Y}$ is calculated as ${\displaystyle \mathrm {H} (Y):=\mathbb {E} [\operatorname {I} (Y)]}$ , i.e.

${\displaystyle \mathrm {H} (Y)=\sum _{y\in {\mathcal {Y}}}{\mathrm {Pr} (Y=y)\,\mathrm {I} (y)}=-\sum _{y\in {\mathcal {Y}}}{p_{Y}(y)\log _{2}{p_{Y}(y)}},}$

where ${\displaystyle \operatorname {I} (y_{i})}$ is the information content of the outcome of ${\displaystyle Y}$ taking the value ${\displaystyle y_{i}}$ . The entropy of ${\displaystyle Y}$ conditioned on ${\displaystyle X}$ taking the value ${\displaystyle x}$ is defined analogously by conditional expectation:

${\displaystyle \mathrm {H} (Y|X=x)=-\sum _{y\in {\mathcal {Y}}}{\Pr(Y=y|X=x)\log _{2}{\Pr(Y=y|X=x)}}.}$

Note that ${\displaystyle \mathrm {H} (Y|X)}$ is the result of averaging ${\displaystyle \mathrm {H} (Y|X=x)}$ over all possible values ${\displaystyle x}$ that ${\displaystyle X}$ may take. Also, if the above sum is taken over a sample ${\displaystyle y_{1},\dots ,y_{n}}$ , the expected value ${\displaystyle E_{X}[\mathrm {H} (y_{1},\dots ,y_{n}\mid X=x)]}$ is known in some domains as equivocation.^[2]

Given discrete random variables ${\displaystyle X}$ with image ${\displaystyle {\mathcal {X}}}$ and ${\displaystyle Y}$ with image ${\displaystyle {\mathcal {Y}}}$ , the conditional entropy of ${\displaystyle Y}$ given ${\displaystyle X}$ is defined as the weighted sum of ${\displaystyle \mathrm {H} (Y|X=x)}$ for each possible value of ${\displaystyle x}$ , using ${\displaystyle p(x)}$ as the weights:^{[3] : 15}

${\displaystyle {\begin{aligned}\mathrm {H} (Y|X)\ &\equiv \sum _{x\in {\mathcal {X}}}\,p(x)\,\mathrm {H} (Y|X=x)\\&=-\sum _{x\in {\mathcal {X}}}p(x)\sum _{y\in {\mathcal {Y}}}\,p(y|x)\,\log \,p(y|x)\\&=-\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}\,p(x)p(y|x)\,\log \,p(y|x)\\&=-\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)\log {\frac {p(x,y)}{p(x)}}.\end{aligned}}}$

Properties [edit]

Conditional entropy equals zero [edit]

${\displaystyle \mathrm {H} (Y|X)=0}$ if and only if the value of ${\displaystyle Y}$ is completely determined by the value of ${\displaystyle X}$ .

Conditional entropy of independent random variables [edit]

Conversely, ${\displaystyle \mathrm {H} (Y|X)=\mathrm {H} (Y)}$ if and only if ${\displaystyle Y}$ and ${\displaystyle X}$ are independent random variables.

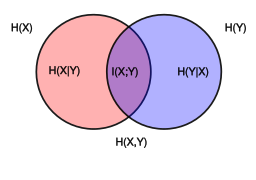
Chain rule [edit]

Assume that the combined system determined by two random variables ${\displaystyle X}$ and ${\displaystyle Y}$ has joint entropy ${\displaystyle \mathrm {H} (X,Y)}$ , that is, we need ${\displaystyle \mathrm {H} (X,Y)}$ bits of information on average to describe its exact state. Now if we first learn the value of ${\displaystyle X}$ , we have gained ${\displaystyle \mathrm {H} (X)}$ bits of information. Once ${\displaystyle X}$ is known, we only need ${\displaystyle \mathrm {H} (X,Y)-\mathrm {H} (X)}$ bits to describe the state of the whole system. This quantity is exactly ${\displaystyle \mathrm {H} (Y|X)}$ , which gives the chain rule of conditional entropy:

${\displaystyle \mathrm {H} (Y|X)\,=\,\mathrm {H} (X,Y)-\mathrm {H} (X).}$ ^{[3] : 17}

The chain rule follows from the above definition of conditional entropy:

${\displaystyle {\begin{aligned}\mathrm {H} (Y|X)&=\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)\log \left({\frac {p(x)}{p(x,y)}}\right)\\[4pt]&=\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)(\log(p(x))-\log(p(x,y)))\\[4pt]&=-\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)\log(p(x,y))+\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}{p(x,y)\log(p(x))}\\[4pt]&=\mathrm {H} (X,Y)+\sum _{x\in {\mathcal {X}}}p(x)\log(p(x))\\[4pt]&=\mathrm {H} (X,Y)-\mathrm {H} (X).\end{aligned}}}$

In general, a chain rule for multiple random variables holds:

${\displaystyle \mathrm {H} (X_{1},X_{2},\ldots ,X_{n})=\sum _{i=1}^{n}\mathrm {H} (X_{i}|X_{1},\ldots ,X_{i-1})}$ ^{[3] : 22}

It has a similar form to chain rule in probability theory, except that addition instead of multiplication is used.

Bayes' rule [edit]

Bayes' rule for conditional entropy states

${\displaystyle \mathrm {H} (Y|X)\,=\,\mathrm {H} (X|Y)-\mathrm {H} (X)+\mathrm {H} (Y).}$

Proof. ${\displaystyle \mathrm {H} (Y|X)=\mathrm {H} (X,Y)-\mathrm {H} (X)}$ and ${\displaystyle \mathrm {H} (X|Y)=\mathrm {H} (Y,X)-\mathrm {H} (Y)}$ . Symmetry entails ${\displaystyle \mathrm {H} (X,Y)=\mathrm {H} (Y,X)}$ . Subtracting the two equations implies Bayes' rule.

If ${\displaystyle Y}$ is conditionally independent of ${\displaystyle Z}$ given ${\displaystyle X}$ we have:

${\displaystyle \mathrm {H} (Y|X,Z)\,=\,\mathrm {H} (Y|X).}$

Other properties [edit]

For any ${\displaystyle X}$ and ${\displaystyle Y}$ :

${\displaystyle {\begin{aligned}\mathrm {H} (Y|X)&\leq \mathrm {H} (Y)\,\\\mathrm {H} (X,Y)&=\mathrm {H} (X|Y)+\mathrm {H} (Y|X)+\operatorname {I} (X;Y),\qquad \\\mathrm {H} (X,Y)&=\mathrm {H} (X)+\mathrm {H} (Y)-\operatorname {I} (X;Y),\,\\\operatorname {I} (X;Y)&\leq \mathrm {H} (X),\,\end{aligned}}}$

where ${\displaystyle \operatorname {I} (X;Y)}$ is the mutual information between ${\displaystyle X}$ and ${\displaystyle Y}$ .

For independent ${\displaystyle X}$ and ${\displaystyle Y}$ :

${\displaystyle \mathrm {H} (Y|X)=\mathrm {H} (Y)}$ and ${\displaystyle \mathrm {H} (X|Y)=\mathrm {H} (X)\,}$

Although the specific-conditional entropy ${\displaystyle \mathrm {H} (X|Y=y)}$ can be either less or greater than ${\displaystyle \mathrm {H} (X)}$ for a given random variate ${\displaystyle y}$ of ${\displaystyle Y}$ , ${\displaystyle \mathrm {H} (X|Y)}$ can never exceed ${\displaystyle \mathrm {H} (X)}$ .

Conditional differential entropy [edit]

Definition [edit]

The above definition is for discrete random variables. The continuous version of discrete conditional entropy is called conditional differential (or continuous) entropy. Let ${\displaystyle X}$ and ${\displaystyle Y}$ be a continuous random variables with a joint probability density function ${\displaystyle f(x,y)}$ . The differential conditional entropy ${\displaystyle h(X|Y)}$ is defined as^{[3] : 249}

${\displaystyle h(X|Y)=-\int _{{\mathcal {X}},{\mathcal {Y}}}f(x,y)\log f(x|y)\,dxdy}$

(Eq.2)

Properties [edit]

In contrast to the conditional entropy for discrete random variables, the conditional differential entropy may be negative.

As in the discrete case there is a chain rule for differential entropy:

${\displaystyle h(Y|X)\,=\,h(X,Y)-h(X)}$ ^{[3] : 253}

Notice however that this rule may not be true if the involved differential entropies do not exist or are infinite.

Joint differential entropy is also used in the definition of the mutual information between continuous random variables:

${\displaystyle \operatorname {I} (X,Y)=h(X)-h(X|Y)=h(Y)-h(Y|X)}$

${\displaystyle h(X|Y)\leq h(X)}$ with equality if and only if ${\displaystyle X}$ and ${\displaystyle Y}$ are independent.^{[3] : 253}

Relation to estimator error [edit]

The conditional differential entropy yields a lower bound on the expected squared error of an estimator. For any random variable ${\displaystyle X}$ , observation ${\displaystyle Y}$ and estimator ${\displaystyle {\widehat {X}}}$ the following holds:^{[3] : 255}

$${\displaystyle \mathbb {E} \left[{\bigl (}X-{\widehat {X}}{(Y)}{\bigr )}^{2}\right]\geq {\frac {1}{2\pi e}}e^{2h(X|Y)}}$$

This is related to the uncertainty principle from quantum mechanics.

Generalization to quantum theory [edit]

In quantum information theory, the conditional entropy is generalized to the conditional quantum entropy. The latter can take negative values, unlike its classical counterpart.

See also [edit]

• Entropy (information theory)
• Mutual information
• Conditional quantum entropy
• Variation of information
• Entropy power inequality
• Likelihood function

References [edit]

1. ^ "David MacKay: Information Theory, Pattern Recognition and Neural Networks: The Book". www.inference.org.uk . Retrieved 2019-10-25 .
2. ^ Hellman, M.; Raviv, J. (1970). "Probability of error, equivocation, and the Chernoff bound". IEEE Transactions on Information Theory. 16 (4): 368–372. doi:10.1109/TIT.1970.1054466.
3. ^ ^{a b c d e f g} T. Cover; J. Thomas (1991). Elements of Information Theory . ISBN0-471-06259-6.

mccarthyowery1942.blogspot.com

Source: https://en.wikipedia.org/wiki/Conditional_entropy

Share this post